Kerneigenschap van de dot.ico serie portretten is optische kleurmenging, en wel zo dat deze een monochrome illusie geeft. Met behulp van de code in mathematica die Jos Hendriks schreef ben ik in staat zwart/wit-beelden om te zetten naar kleurenbeelden die als basis voor mijn portretten dienen. De werkvolgorde om tot een geschilderd portret te komen is in 4 stappen
1 – Zwart/wit-foto
2 – Omzetting naar kleur
3 – Bewerking in Photoshop
4 – Schilderij
The core property of the dot.ico series of portraits is optical color mixing, in such a way that it gives a monochrome illusion. With the help of the code in mathematics that Jos Hendriks wrote, I am able to convert black/white images to color images that serve as the basis for my portraits. The sequence of work to arrive at a painted portrait is in 4 steps
1 - Black/white photo
2 - Conversion to color
3 - Editing in Photoshop
4 - Painting

Detail portret Ariëlle, grijswaarden omgezet naar kleur in Mathematica
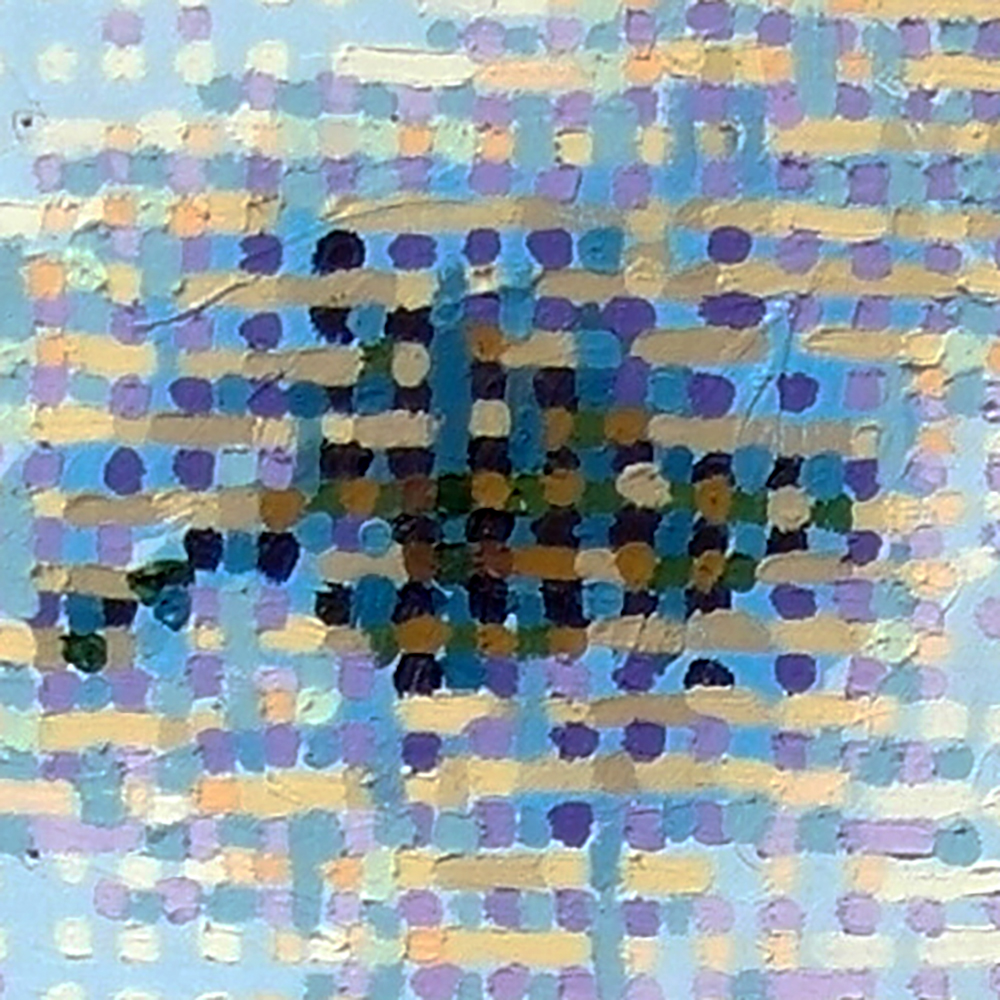
Detail Schilderij
–
Uitleg van de schrijver van de code: Jos Hendriks | explanation of the creator of the code: Jos Hendriks
Stel je voor:
Je komt een ruime kamer binnen. Aan de muur tegenover de zijde van de kamer waar je binnen komt hangt een portret. Een zwart-wit portret. Het is een goed gelijkend portret en er schemert iets door van het karakter van de afgebeelde persoon. Je loopt naar het portret toe. Terwijl je er naar toe loopt zie je het portret langzaam uiteenvallen in kleurrijke blokjes. Dicht bij het schilderij, want dat is het, is er geen portret meer te zien, en kijk je naar een kleurrijk abstract kunstwerk.Dit wilde, zo vertelde Luuk mij, zo’n 20 jaar geleden, toen hij bij mij logeerde in Frankrijk, bereiken. Toen hij dit vertelde, realiseerde ik mij, in een flits, dat ik hem hierbij kon helpen door het schrijven van een computerprogramma dat een handleiding bood hoe te werk te gaan. Luuk is een ambachtelijke schilder, maar hij had me ook wel eens verteld dat het hem interressant leek om moderne technieken te gebruiken in zijn werk. Dat kwam dus goed uit.
Mijn gedachte was dit: “ Het moet kunnen met behulp van magische vierkanten”.
Magische vierkanten zijn vierkante blokken gevuld met getallen. Er zijn evenveel kolommen als rijen. En er is een speciale eigenschap. Dit is een voorbeeld:

Imagine:
You enter a spacious room. On the wall opposite the side of the
room you enter, there is a portrait. A black and white portrait. It is
a good likeness and something of the character of the person depicted shines through. You walk towards the portrait.
As you walk towards it,
you see the portrait slowly disintegrate into colourful blocks. Close to the painting, because that is what it is, there is no portrait to be seen, and you are looking at a
colourful abstract work of art.
This is what Luuk told me about 20 years ago, when he was staying with me in France.
When he told me this, I realised, in a flash, that I could help him with this by writing a computer programme that offered a manual on how to go about it.
Luuk is a craftsman painter, but he had also told me that he thought it would be interesting to use modern techniques in his work. That worked out well. My thought was this: “It must be possible with the help of magic squares”.
Magic squares are square blocks filled with numbers. There are
as many columns as rows. And there is a special property. This is an
example:
De speciale eigenschap: De som van de getallen in iedere rij en in iedere
kolom en de som van de getallen op de twee diagonalen is steeds hetzelfde. In het voorbeeld is die som 34. Magisch vierkanten horen thuis in de zogenaamde recreatieve wiskunde. Ondanks dat zijn er vele serieuze artikelen over verschenen waar vragen als: hoeveel zijn er van een bepaalde grootte? Zijn er met extra eigenschappen? bestaan er magische vierkanten waar alle getallen kwadraten zijn? enz. Om te laten zien hoe je magische vierkanten kunt gebruiken moet ik eerst laten zien hoe een beeld, ieder beeld, ieder plaatje op een beeldscherm wordt getoverd.Een beeldscherm is opgebouwd uit puntjes. Deze puntjes worden pixels genoemd. Hoe meer pixels hoe scherper een beeld op dat scherm kan zijn. Tv schermen, monitoren, telefoonschermen hebben zo tussen de 500 en2000 pixels horizontaal en ook iets dergelijks verticaal. Voor dit verhaal gaan we uit van 1000 pixels horizontaal en 1000 pixels verticaal. Dat zijn in het totaal 1000×1000= 1 miljoen pixels. Naar iedere pixel worden drie lichtstralen gestuurd, Een straal met een zekere hoeveelheid rood licht, een straal met een bepaalde hoeveelheid groen licht en een straal met een hoeveelheid blauw licht. In de pixel worden deze stralen gemengd en dat bepaald de kleur van de pixel. De hoeveelheid rood, groen en blauw dat naar de pixel wordt gestuurd wordt beschreven met een geheel getal van 0 tot en met 255. Nul betekent helemaal geen licht, 255 maximale sterkte. Nu kunnen
we met 3 getallen de kleur beschrijven, die naar de pixel wordt gestuurd. Voorbeelden:
The special property: The sum of the numbers in each row and in each
column and the sum of the numbers on the two diagonals is always the same. In the example, that sum is 34.
Magic squares belong in so-called recreational mathematics.
Despite that, many serious articles have been published on the subject where questions such as:
how many are there of a certain size? Are there any with extra properties?
do magic squares exist where all numbers are squares? etc.
To show how you can use magic squares, I must first show how an image, every image, every picture is conjured up on a screen.A screen is made up of dots. These dots are called pixels. The more pixels, the sharper an image on that screen can be.
TV screens, monitors, telephone screens have between 500 and 2000 pixels horizontally and something like that vertically. For this story, we assume 1000 pixels horizontally and 1000 pixels vertically. That is a total of 1000x1000 = 1 million pixels. Three light rays are sent to each pixel, a ray with a certain amount of red light, a ray with a certain amount of green light and a ray with a certain amount of blue light.
These rays are mixed in the pixel and that determines the color of the pixel. The amount of red, green and blue that is sent to the pixel is described with an integer from 0 to 255. Zero means no light at all, 255 maximum strength.
Now we can describe the color that is sent to the pixel with 3 numbers.
Examples:
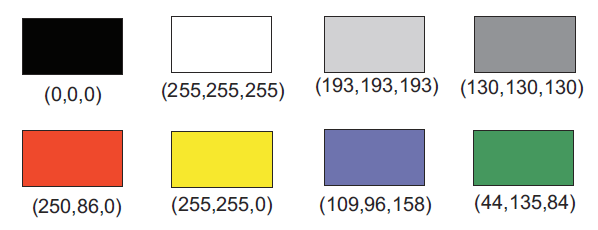
Wanneer de maximale hoeveelheid licht van alle drie de kleuren naar de pixel wordt gestuurd (255,255,255), ontstaat wit licht. Als de lichtsterkte van alle drie de stralen hetzelfde is, dus alle drie de getallen hetzelfde zijn, ontstaat grijs. Hoe hoger de waarde, hoe lichter de kleur. (193,193,193) is tamelijk licht grijs en (130,130,130) is wat donkerder grijs.
Bij een beeldscherm wordt het beeld meestal 60 keer per seconde ververst. Dus 60 keer per seconde worden nieuwe lichtstralen, gedefinieerd door nieuwe getal tripels naar ieder van, de in ons voorbeeld een miljoen pixels,
gestuurd. Bij deze verversingwaarde zien bewegingen er natuurlijk uit. Nogal indrukwekkend, lijkt me.
Voor nu is niet zo zeer het beeldscherm maar een plaatje op het beeldscherm van belang. Dan is verversing niet nodig. We nemen een kleine zwart-wit foto van 24×24 pixels:
When the maximum amount of light of all three colours is sent to the pixel (255,255,255), white light is created. If the light intensity of all three rays is the same, so all three numbers are the same, grey is created. The higher the value, the lighter the colour. (193,193,193) is fairly light grey and (130,130,130) is somewhat darker grey.
A screen usually refreshes the image 60 times per second.
So 60 times per second new light rays, defined by new number triples, are sent to each of the, in our example, one million pixels.
At this refresh value, movements look natural. Quite impressive, I think.
For now, it is not so much the screen but an image on the screen that is important. Then refreshing is not necessary. We take a small black and white photo
of 24×24 pixels:

Hoe groot dat op uw beeldscherm is hangt af van het aantal pixels dat u
beeldscherm heeft en het kan er anders uit zien op mijn en op uw scherm. Maar intern, in het geheugen van de computer, telefoon etc. ziet het plaatje er hetzelfde uit:
How big that is on your screen depends on the number of pixels your
screen has and it can look different on mine and your screen.
But internally, in the memory of the computer, phone etc. the picture
looks the same:
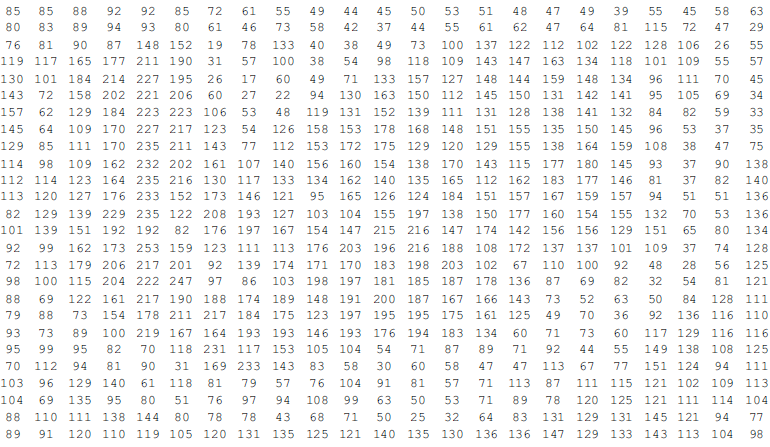
Dit zijn 24×24 getallen, voor iedere pixel een getal. Zij bepalen de hoeveelheid rood dat naar de pixels wordt gestuurd. Er zijn ook 24×24 getallen, die voor iedere pixel de hoeveelheid groen bepalen en een derde keer 24×24 getallen voor de blauwe component. In dit geval zijn die schema’s hetzelfde voor alle drie de kleuren omdat het een zwart-wit plaatje is. Het idee is nu om de getallen in deze schema’s te gaan manipuleren. We gaan bij alle getallen in deze schema’s iets optellen of iets aftrekken, maar doen dat zo dat de veranderingen in de direkte omgeving van een getal elkaar, laten we zeggen, uitdoven. En hier kunnen we handig magische vierkanten voor gebruiken. Daartoe moeten we eerst een magisch vierkant wat veranderen. We maken alle getallen eerst twee keer zo groot. Het magisch vierkant blijf dan een magisch vierkant. En vervolgens trekken we de gemiddelde waarde van alle getallen, van ieder getal af. Hierdoor wordt de som van de getallen in een rij of een kolom of op een diagonaal altijd 0 is. Ook nu blijft het vierkant magisch.
These are 24x24 numbers, a number for each pixel. They determine the amount of red that is sent to the pixels. There are also 24x24 numbers, which determine the amount of green for
each pixel and a third time 24x24 numbers for the blue component. In this case, these schemes are the same for allthree colors because it is a black and white image. The idea now is to manipulate the numbers in these schemes. We are going to add or subtract something from all the numbers in these schemes, but do so in such a way that the changes in the direct environment of a number, let's say, cancel each other out. And for this we can conveniently use magic squares. To do this, we first have to change a magic square a little. We
first make all the numbers twice as big.
The magic square then remains a magic square. And then we subtract the average value of all the numbers from each number. This means that the sum of the numbers in a row or column or on a diagonal is always 0. The square remains magical.
het magisch vierkant waar we
mee beginnen A:
the magic square we
start with A:

wordt dan eerst
B: alle getallen x2
then first becomes
B: all numbers x2

en vervolgens C: alle getallen -17
and then C: all numbers -17

Hier is hetzelfde portret
weergegeven. Elk vierkantje stel nu
een pixel voor.
Here is the same portrait
shown. Each square now represents
a pixel.

We nemen de eerste 4 bij 4 pixels links boven:
We take the first 4 by 4 pixels at the top left:

en de daarbij behorende getallen:
and the corresponding numbers:

We gaan de getallen, die in het nieuwe schema staan, gebruiken voor de hoeveelheid rood licht dat naar de 16 pixels rechtsboven in de foto wordt gestuurd. De hoeveelheid rood licht veranderd in alle pixels, maar de hoeveelheid rood licht wat naar de rijen en kolommen en diagonalen wordt gestuurd blijft hetzelfde. Bijvoorbeeld:
In de oorspronkelijke eerste rij 89+91+120+110= 410 en dat wordt
74+98+131+107=410 in de nieuwe eerste rij.
We are going to use the numbers in the new diagram for the
amount of red light that is sent to the 16 pixels at the top right of the photo.
The amount of red light changes in all pixels, but the amount of red light
that is sent to the rows and columns and diagonals remains the same.
For example:
In the original first row 89+91+120+110= 410 and that becomes
74+98+131+107=410 in the new first row.

Hier worden dus de getallen, die op overeenkomstige plaatsen staan bij
elkaar opgeteld. Het moeilijkste hebben we nu gehad. Verder is het een kwestie van heel veel herhalen. We kunnen dit proces namelijk op ieder blokje van 16 pixels uitvoeren en zo alle hoeveelheden rood licht dat naar de pixels wordt gestuurd veranderen en er wel voor zorgen dat de hoeveelheid rood licht in de direkte omgeving van iedere pixel hetzelfde blijft. Wat die direkte
omgeving is wordt bepaald door de grootte van het magisch vierkant wat
we gebruiken. We geven nu een voorbeeld van het fotootje van hierboven, maar nu van 48 bij 48 pixels als we deze foto veranderen met behulp van het magisch vierkant C:
Here the numbers that are in corresponding places are added together. We have now had the hardest part. Furthermore it is a matter of a lot of repetition. We can perform this process on every block of 16 pixels and thus change all the amounts of red light that is sent to the pixels and ensure that the amount of red light in the immediate vicinity of each pixel remains the same. What that immediate vicinity is is determined by the size of the magic square that we use.
We now give an example of the photo above, but now of 48 by 48 pixels if we change this photo using the magic square C:


We gaan deze foto nu bewerken met de hulp van het magisch vierkant
waarmee we zijn begonnen:
Now we are going to edit this photo with the help of the magic square we started with:

Maar voor een wat sterker effect vermenigvuldig we het met een factor 6:
But for a slightly stronger effect we multiply it by a factor of 6:
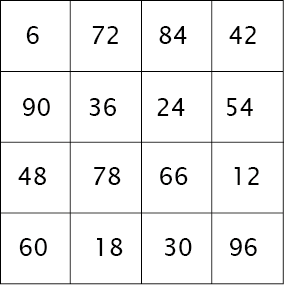
dat we herleiden zodat de gemiddelde verandering over rijen, kolommen en diagonalen 0 is
that we reduce so that the average change over rows, columns and diagonals is 0
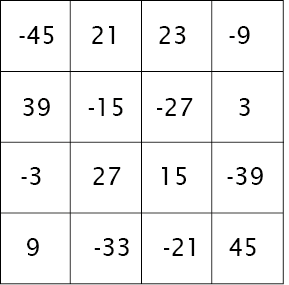
En dit schema gebruiken we om de hoeveel rood dat naar de pixels wordt gestuurd te veranderen.
Voor het veranderen van de hoeveelheid groen gebruiken we het schema waarbij de rijen en kolommen van het schema hierboven zijn verwisseld. Ook hierdoor blijft het een magisch vierkant.
And we use this scheme to change the amount of red that is sent to the pixels.
To change the amount of green, we use the scheme where the rows and columns of the scheme above are swapped. This also keeps it a magic square.
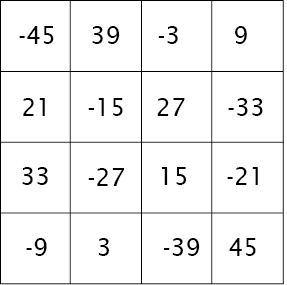
en voor de component groen gebruiken we een schema waarbij de rijen kolommen op een nog wat andere manier zijn gemanipuleerd
and for the green component we use a scheme where the rows and columns are manipulated in a slightly different way
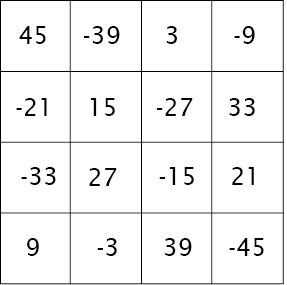
We moeten voor de drie kleurcomponenten verschillende magische vierkanten gebruiken omdat als we dezelfde gebruiken welliswaar de kleur verandert, maar de grijswaarden blijven. Resultaat:
We need to use different magic squares for the three color components because if we use the same ones, the color will change, but they will remain grayscale.
Result:


Geef een reactie